graph LR
X1(X1) --> W1(w1)
X2(X2) --> W2(w2)
X3(X3) --> W3(w3)
Xn(Xn) --> Wn(wn)

subgraph Sum
    Z(∑ f)
end

W1 ---> Z
W2 ---> Z
W3 ---> Z
Wn ---> Z

Z --> Y1(y1)

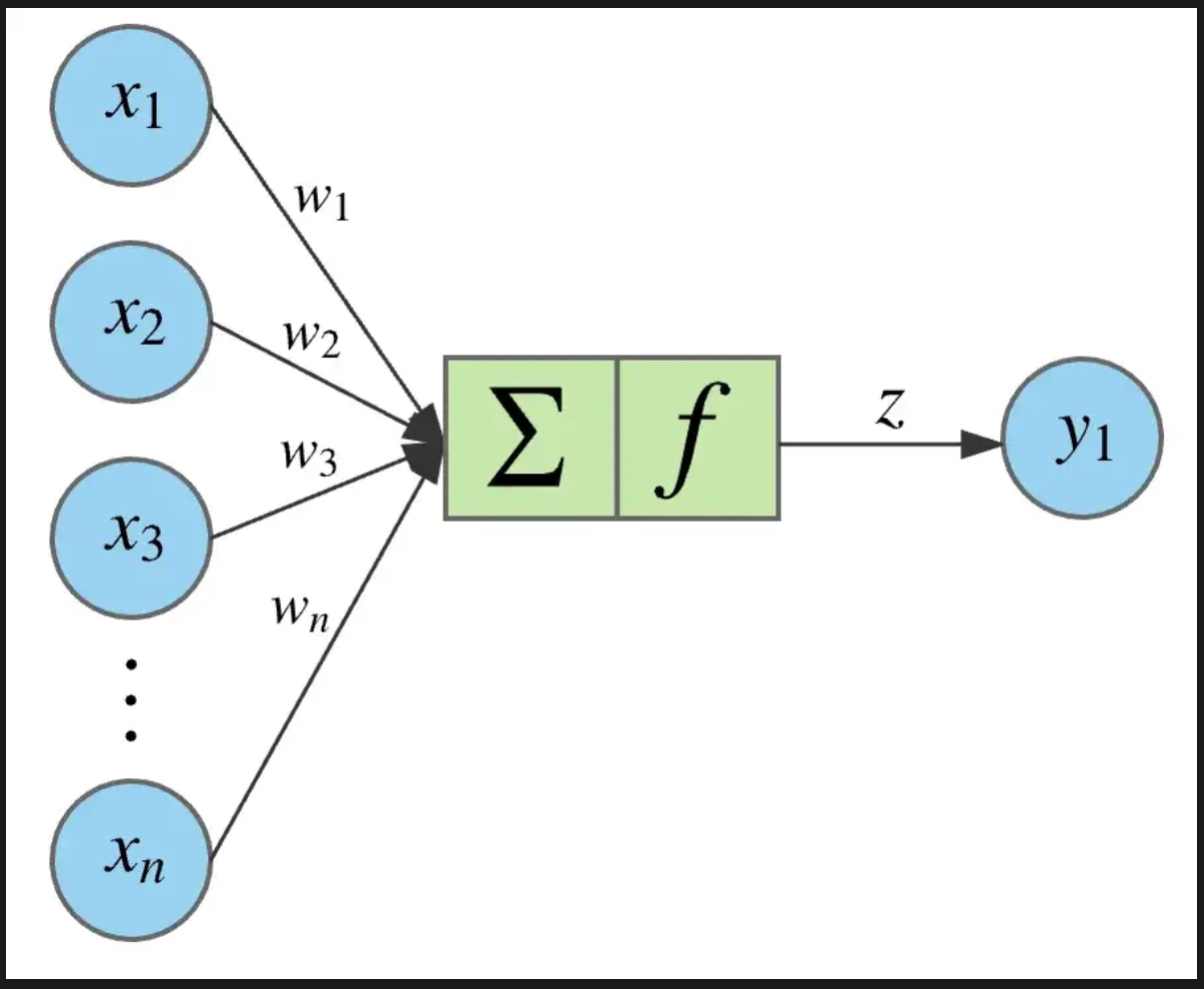
Forward Pass

out = $f\left(b + \sum_i x_i \cdot w_i\right) = f\left(b + x w^T\right)$

• $x_i$ ... Input features
• $w_i$ ... Weights, Parameter
• $b$ ... Bias
• $f$ ... Activation function

Erklärung: Jedes Input-Feature $x_i$ wird mit einem Gewicht $w_i$ multipliziert. Diese Produkte werden aufsummiert, und es wird ein Bias $b$ hinzugefügt. Das Ergebnis wird dann durch eine Aktivierungsfunktion $f$ geleitet, um die Ausgabe zu erzeugen.

BACKPROPAGATION

The weight update formula is given by:

$w_{t+1} = w_t - \eta \frac{\partial L}{\partial w_t}$

Where:

• $\eta$ is the learning rate
• $L$ is the loss function
• $\frac{\partial L}{\partial w_t}$ is the gradient of the loss with respect to the weights at time step $t$

Erklärung: Das neue Weight $w_{t+1}$ ist das alte Weight $w_t$ minus $\eta \frac{\partial L}{\partial w_t}$

Dies bedeutet, dass die Weights in Richtung des negativen Gradienten der Verlustfunktion angepasst werden, um den Fehler zu minimieren.

Adam Optimizer

Die Backpropagation berechnet die Gradienten (die Ableitung des Fehlers), und Adam verwendet diese Gradienten, um die Gewichte effizient und adaptiv anzupassen.

Batch Size

Die Batch Size gibt an, wie viele Trainingsbeispiele in einem einzigen Vorwärts- und Rückwärtsdurchlauf durch das Netzwerk verarbeitet werden.

Normalerweise wird die Batch Size als Potenz von 2 gewählt (z.B. 32, 64, 128), da dies die Berechnungen auf GPUs optimiert.

Klassifikation vs. Regression

• Klassifikation: Kategorien zuweisen (z.B. Katze, Hund, Auto)
• Regression: Kontinuierliche Werte vorhersagen (z.B. Preis, Temperatur)

Klassifikation

kann binär (z.B. Ja/Nein) oder multi-klassig (z.B. Katze/Hund/Auto) sein.

• binär: Sigmoid
• multi-klassig: Softmax

Warum Softmax und nicht auch Sigmoid?

Sigmoid gibt für jede Klasse eine Wahrscheinlichkeit zwischen 0 und 1 zurück, unabhängig von den anderen Klassen. Dies kann zu inkonsistenten Ergebnissen führen, da die Wahrscheinlichkeiten nicht notwendigerweise zusammen 1 ergeben.

Bei jeder observation weights updaten problematisch

• viel Aufwand
• ständig auf/ab
• ein paar processen, Fehler mitteln

Begriffe Erklärt

Bias

Der Bias $b$ verschiebt die Aktivierungsfunktion.

Warum: Ohne Bias müsste das Neuron durch den Ursprung gehen, was die Flexibilität des Modells einschränkt.