Schwingungen

Periodischer Vorgang, der relgelmässig wiederholt wird. Kann, muss aber nicht mit Bewegung zu tun haben. (z.B. Magnetismus).

Grundwissen

Amplitude: Maximale Auslenkung eines Oszillators. ("Höhe" der Schwingung)
Frequenz: Anzahl der Schwingungen pro Sekunde. (Hz)
Periode: Zeit, die eine Schwingung dauert. (s)
Kreisfrequenz: Winkelgeschwindigkeit eines Oszillators. ( $\omega$ )
Phase: Zeitpunkt, an dem eine Schwingung beginnt. (Winkel)
Schwingungsdauer: Zeit, die eine Schwingung dauert. (s)
Schwingungsfrequenz: Anzahl der Schwingungen pro Sekunde. (Hz)
Schwingungsgleichung: Mathematische Beschreibung einer Schwingung.
Schwingungszustand: Zustand eines Oszillators zu einem bestimmten Zeitpunkt.
Schwingungszustandsgleichung: Mathematische Beschreibung eines Schwingungszustands.
Winkelgeschwindigkeit: Geschwindigkeit, mit der sich ein Oszillator dreht. ( $\omega$ )

Periodendauer $T$ und Frequenz $f$

Die kürzeste Zeit, zwischen zwei exakt gleichen Zuständen, wird als Periodendauer $T$ bezeichnet. Die Frequenz $f$ ist die Anzahl der Schwingungen pro Sekunde. $f = \frac{1}{T}$

Winkelgeschwindigkeit $\omega$

Die Winkelgeschwindigkeit $\omega$ gibt an, wie schnell sich ein Objekt um einen bestimmten Winkel dreht. Sie wird in $s^{-1}$ gemessen. $\omega = 2\pi f = \frac{2\pi}{T} = \frac{\Delta \phi}{\Delta t}$ Schwingung, Funktion y, siehe Buch.

y(t)=2\sin \left( \frac{2\pi}{4} t + \frac{\pi}{6} \right)

wie kommt man auf $\frac{\pi}{6}$ ? $(ax+b)$ vs $a(x+b)$ $\frac{2\pi}{4}\left( x+\frac{1}{3} \right)$ wenn man eine abbildung hat, und $a*\sin (bx+c)+d$ ablesen muss, bedenken dass man a, b und d ablesen kann, c nicht, wenn man $a(x+b)$ nimmt, kann man den "offset" in vielfachen der schwingung sehen

ka

Oszillator: ein schwingungsfähiges system harmonischer Oszillator: ein Oszillator bei dem die Bewegung durch eine Sinus(Kosinus))-Funktion beschrieben werden kann.

Federpendel

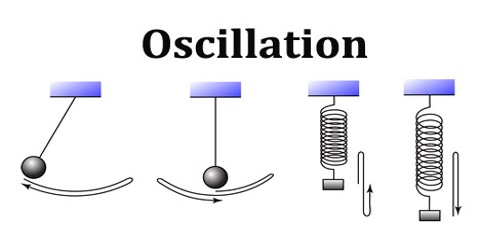
Oszilation img.

eine Feder ist ein harmonischer Oszillator, wenn sie elastisch ist. Die Federkonstante gibt an, wie stark die Feder ist. Je weiter die Feder vom Gleichgewichtszustand entfernt ist, desto stärker ist die Rückstellkraft.

eine Feder ist ein harmonischer Oszillator, wenn sie elastisch ist. Die Federkonstante gibt an, wie stark die Feder ist. Je weiter die Feder vom Gleichgewichtszustand entfernt ist, desto stärker ist die Rückstellkraft.

Formel zur Berechnung der Frequenz $f$ eines Federpendels:

f = \frac{1}{2\pi} \sqrt{\frac{k}{m}}

$f$ : Frequenz (Schwingungen pro Sekunde)
$k$ : Federkonstante (N/m)
$m$ : Masse (kg)

Erklärung: Die Frequenz $f$ ist umgekehrt proportional zur Wurzel der Masse $m$ und der Federkonstante $k$ . d.h. je grösser die Masse oder die Federkonstante, desto kleiner die Frequenz.

Pendel

Ein Pendel funktioniert mithilfe der Schwerkraft. Die Pendellänge $l$ ist die Distanz zwischen dem Aufhängepunkt und dem Schwerpunkt des Pendels. Die Pendelmasse $m$ ist die Masse des Pendels.

Formel zur Berechnung der Frequenz $f$ eines Pendels ist gleich der Frequenz eines Federpendels:

f = \frac{1}{2\pi} \sqrt{\frac{g}{l}}

$f$ : Frequenz (Schwingungen pro Sekunde)
$g$ : Erdbeschleunigung (m/s^2)
$l$ : Pendellänge (m)

Beispiel: Ein Turm in Taipeh, Taiwan, besitzt ein Pendel zur Stabilisierung. Die Pendellänge beträgt 14m und das GEwicht 660 Tonnen.

Berechne die Frequenz des Pendels.

Lösung:

g = 9.81 m/s^2
l = 14m

f = \frac{1}{2\pi} \sqrt{\frac{9.81}{14}} = 0.13 Hz

Für die Periodendauer ergibt das: $T = \frac{1}{f} = 7.5s$

Überlagerung von Schwingungen

Entweder in der selben Richtung oder aufeinander senkrecht.

Begriffe

Unabhängigkeitsprinzip: Zwei Schwingungen, die sich in der selben Richtung bewegen, können unabhängig voneinander betrachtet werden.
Superpositionsprinzip: Die resultierende Schwingung ist die Summe der einzelnen Schwingungen.
Interferenz: Die Überlagerung von zwei Schwingungen, die sich in der selben Richtung bewegen.
Stehende Welle: Eine Welle, die sich nicht bewegt.
Wellenlänge: Die Distanz zwischen zwei Wellenbergen.
Wellenamplitude: Die maximale Auslenkung einer Welle.
Wellengeschwindigkeit: Die Geschwindigkeit, mit der sich eine Welle bewegt.

senkrechte Schwingungen

Wenn zwei Schwingungen aufeinander senkrecht sind, können sie als Vektoraddition betrachtet werden. Die resultierende Schwingung ist die Summe der beiden Schwingungen. Die Amplitude der resultierenden Schwingung ist die Länge des Vektors.

Gedämpfte Schwinung

Durch Luftwiderstand oder Reibung wird die Schwingung allmählich schwächer. Die Amplitude nimmt ab und die Frequenz bleibt konstant.

y(t) = y_0 * e^{-\gamma t} \sin(\omega _D * t)

$y(t)$ : Auslenkung zur Zeit $t$
$y_0$ : Anfangsauslenkung
$\gamma$ : Dämpfungskonstante
$\omega _D$ : Dämpfungsfrequenz
$t$ : Zeit

Der Kriechfall

Wenn die Dämpfung so stark ist, dass das System nicht mehr zurückschwingt und in den Ruhezustand zurückkehrt spricht man vom Kriechfall.

Bei einem Auto würde das bedeuten, dass die Federung so stark gedämpft ist, dass das Auto nicht mehr auf und ab hüpft, was zu einem angenehmeren Fahrgefühl führt. Wichtig ist, dass das Auto nicht zu stark gedämpft ist, da es sonst zu einem harten Fahrgefühl führen würde (Die Dämpfung würde die Schwingungen nicht mehr abfedern ≈ keine Federung).

Erzwungene Schwingung

Eine Schwingung, die durch eine äussere Kraft erzwungen wird. Die Frequenz der erzwungenen Schwingung ist die Frequenz der äusseren Kraft.

zB. Schaukel, die durch das Schaukeln oder antauchen in Bewegung versetzt wird.

Resonanz

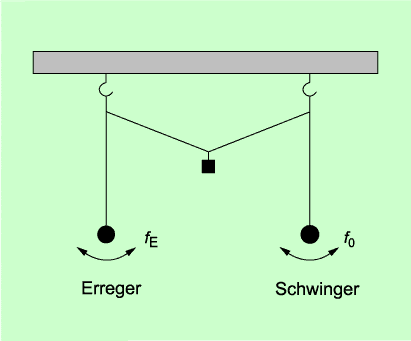
Resonanz img

Wenn die Frequenz der erzwungenen Schwingung gleich der Eigenfrequenz des Systems ist, spricht man von Resonanz. Das System beginnt zu schwingen und die Amplitude nimmt zu.

zB. Glas, das durch eine Stimmgabel zum Schwingen gebracht wird.

Wenn die Frequenz der erzwungenen Schwingung größer oder kleiner ist als die Eigenfrequenz des Systems wird die Schwingung ständig gedämpft und die Amplitude nimmt ab.

zB. Schaukel, die durch das Schaukeln oder antauchen in Schwingung versetzt wird, dann aber durch zu früh oder zu spätes antauchen wieder zum Stillstand kommt.

Musikinstrumente sind so konstruiert, dass sie bei möglichst vielen Frequenzen schwingen. Dadurch können sie viele Töne erzeugen.

Formel Übersicht

Periodendauer $T$ und Frequenz $f$ $f = \frac{1}{T}$
Winkelgeschwindigkeit $\omega = 2\pi f = \frac{2\pi}{T} = \frac{\Delta \phi}{\Delta t}$
Federpendel $f = \frac{1}{2\pi} \sqrt{\frac{k}{m}}$
Pendel $f = \frac{1}{2\pi} \sqrt{\frac{g}{l}}$
Gedämpfte Schwingung $y(t) = y_0 * e^{-\gamma t} \sin(\omega _D * t)$

Schall

Infraschall

Schallwellen mit einer Frequenz unterhalb des hörbaren Bereichs (unter 20 Hz).

Ultraschall

Schallwellen mit einer Frequenz oberhalb des hörbaren Bereichs (über 20 kHz).

Musik

Tonhöhe: Die Frequenz eines Tons bestimmt die Tonhöhe.
Klang (Timbre): Die Obertöne bestimmen den Klang eines Tons.
Lautstärke: Die Amplitude eines Tons bestimmt die Lautstärke.

zwei phasenverschobene Töne gleicher Frequenz u. Amplitude

Gleichphasig: Die Töne werden lauter.
Gegenphasig: Die Töne heben sich auf.

Obertöne

Die Obertöne bestimmen den Klang eines Tons. Sie sind ganzzahlige Vielfache der Grundfrequenz.

zB. Ein Ton mit der Frequenz 100 Hz hat Obertöne bei 200 Hz, 300 Hz, 400 Hz, usw.

In der Musik sind das der Grundton, die Oktave, die Quinte, die Terz, usw.

Die Obertonreihe ist eine Reihe von Tönen, die durch die Obertöne eines Grundtons entstehen.

Kopplung von Pendeln

Zwei Pendel sind gekoppelt, wenn sie durch eine Feder oder eine Schnur miteinander verbunden sind. Die Kopplung kann symmetrisch oder asymmetrisch sein.

Symmetrische Kopplung: Die Pendel schwingen in Gegenphasen.
Asymmetrische Kopplung: Die Pendel schwingen in Gleichphasen.

Ist die Kopplung asymmetrisch, so kann es zu Schwebungen kommen. Das bedeut das die Pendel sich abwechselnd beschleunigen und bis zum Stillstand abbremsen.

Bsp.:

y(t) = A \sin(\omega t + \phi)

Frequenz f und Kreisfrequenz $\omega$

Die Frequenz $f$ gibt an, wie oft sich ein Pendel pro Sekunde bewegt.

Die Kreisfrequenz $\omega$ gibt an, wie schnell sich ein Pendel um einen bestimmten Winkel dreht.

f = \frac{1}{T}

Die Kreisfrequenz $\omega$ ist die Strecke eines Kreises mit Radius 1, die in einer Sekunde zurückgelegt wird.

\omega = 2\pi f = \frac{2\pi}{T}